Ejercicios de Distribución Binomial

 

Ejercicio 1:

La probabilidad de que a un cliente nuevo le guste la matehamburguesa de Jorge es de 0,8. Si llegan 5 clientes nuevos a la cafetería, ¿cuál es la probabilidad de que solo a 3 de ellos les guste la matehamburguesa?

Solución:

Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.

En este caso, vamos a centrarnos en los clientes a los que les gusta esta hamburguesa, por ello diremos que:

X = número de clientes nuevos de 5 a los que les gusta la matehamburguesa

Entonces consideramos un éxito si al cliente le gusta esta hamburguesa.

Aplicaremos la fórmula binomial:

Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito.

Reemplazamos estos valores en la fórmula:

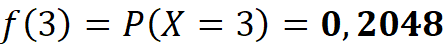
La respuesta sería 0,2048.

Ejercicio 2:

De todas las flores plantadas por una empresa de jardinería, el 90% sobrevive. Si se plantan 10 flores ¿cuál es la probabilidad de que 9 o más sobrevivan?

Solución:

Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.

En este caso, vamos a centrarnos en las flores que sobreviven, por ello diremos que:

X = número de flores de 10 que sobreviven

Entonces consideramos un éxito si la flor sobrevive. A las que flores que se mueren, las consideramos como un fracaso.

Aplicaremos la fórmula binomial:

Nos piden calcular la probabilidad de 9 o más sobrevivan.

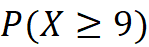
Este problema tiene trampa, porque dado que se plantaron 10 flores, la máxima cantidad de flores que pueden sobrevivir es 10, por lo tanto:

– ¿Y no pueden sobrevivir 11 flores?
– No se puede, porque solo se plantaron 10.
– ¿Y si las flores tienen hijitos bonitos?
– Alumno por favor, tome menos azúcar. Concéntrese y sigamos con la clase.

Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito. En este caso:

Regresamos con la fórmula de arriba:

Vamos a calcular cada probabilidad por separado, empezando con P(X = 9):

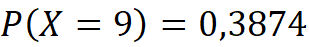
Continuamos con P(X = 10).

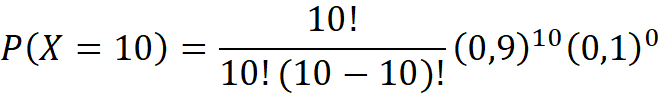
Regresamos con esta fórmula:

Y reemplazamos lo calculado:

Ejercicio 3:

Considere un experimento binomial con dos ensayos y p=0,4.
a) Calcular la probabilidad de no obtener ningún éxito.
b) Calcular la probabilidad de obtener al menos 1 éxito.

Solución:

Iniciamos definiendo la variable aleatoria de interés en nuestro experimento binomial:

X = número de éxitos en n ensayos.

x = 0; 1; 2.

El enunciado nos dice que: n = 2 y que p = 0,4; con ello podemos definir la función de probabilidad de X.

a) Calcular la probabilidad de no obtener ningún éxito: P(X = 0).

b) Calcular la probabilidad de obtener al menos 1 éxito.

Aquí nos piden calcular:

Pero:

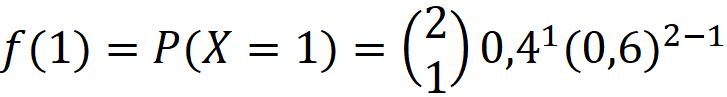
Además:

Reemplazamos:

Esa sería la respuesta: 0,64.

Ejercicio 4:

 

         

Ejercicio 5:

 

 

Referencias Bibliograficas

-https://www.vadenumeros.es/sociales/ejemplos-distribucion-binomial.htm

-https://matemovil.com/distribucion-binomial-ejercicios-resueltos/