Experimento aleatorio: concepto, espacio muestral, Regla de la suma o adición de probabilidades y Reglas de Multiplicación
Experimento aleatorio: concepto, espacio muestral, ejemplos
Se habla de experimento aleatorio cuando el resultado de cada ensayo particular es impredecible, aun cuando se pueda establecer la probabilidad de ocurrencia de determinado resultado.
Sin embargo, habría que aclarar que no es posible reproducir el mismo resultado de un sistema aleatorio con los mismos parámetros y condiciones iniciales en cada ensayo del experimento.

Un buen ejemplo de un experimento aleatorio es el lanzamiento de un dado. Aun cuando se tenga el cuidado de lanzar el dado de la misma manera, en cada intento se obtendrá un resultado impredecible. Realmente, lo único que puede afirmarse es que el resultado puede ser alguno de los siguientes: 1, 2, 3, 4, 5 o 6.
El lanzamiento de una moneda, es otro ejemplo de experimento aleatorio con solo dos resultados posibles: cara o sello. Aunque la moneda se lance desde la misma altura y de la misma manera, siempre el factor azar estará presente, lo que resulta en incertidumbre a cada nuevo intento.
Lo contrario de un experimento aleatorio es un experimento determinista. Por ejemplo, se sabe que cada vez que se hierve agua a nivel del mar la temperatura de ebullicción es 100 ºC. Pero nunca ocurre que, manteniendo las mismas condiciones, el resultado sea a veces 90 ºC, otras 12 0ºC y a veces 100 ºC.
Espacio Muestral
De acuerdo con el concepto suministrado por la la estadística de probabilidades, el espacio muestral es, de forma general, el conjunto de resultados posibles que deriven de un experimento aleatorio. Es importante tener en cuenta que, los experimentos aleatorios, son aquellas pruebas que, siguiendo un patrón constante de características o de condiciones iniciales, pueden derivar en una gama de resultados completamente diferentes entre sí; por ello, se le suele definir como aquellos experimentos cuyos resultados no pueden ser previstos. Con estos conceptos se relaciona, igualmente, aquel del evento aleatorio, el conjunto de resultados, como tal, que pueden venir de un experimento aleatorio.
La teoría de probabilidades, la rama de la matemáticas que da vida a al muestreo o espacio muestral, es aquella encargada de analizar todos aquellos eventos estocásticos y aleatorios, que resultan como consecuencia de diversas pruebas o experimentos. El espacio muestral son, como ya se explicó anteriormente, los eventos posibles. Así, cuando se realiza un experimento en el que se deben lanzar dos monedas al aire, el muestreo se reduciría a los conjuntos: {(cara, cara), (cara, cruz), (cruz, cara) y (cruz, cruz)}. A partir de esto aparecen los eventos o sucesos, los subconjuntos de los espacios muestrales, que a su vez pueden convertirse en sucesos elementales cuando sólo tienen un elemento de importancia.
Ejemplos:
Algunos experimentos requieren de la existencia de dos espacios muestrales, puesto que tiene dos elementos que pueden determinar los eventos. Un ejemplo de estos son los experimentos con cartas; en estos, un espacio de muestreo está dedicado al posible número a aparecer (desde el as hasta el Rey), además de aquél relacionado con el mazo, que puede variar de acuerdo al tipo de baraja que se emplee.
D = {1, 2, 3, 4, 5, 6}.
Por su parte, en el lanzamiento de una moneda el espacio muestral es:
M ={cara, sello}.
Regla de la suma o adición de probabilidades
Veamos como sumar probabilidades, ya sea que los eventos sean mutuamente excluyentes o no.
La regla de adición o regla de la suma, establece que si tenemos un evento A y un evento B, la probabilidad de que ocurra el evento A o el evento B se calcula de la siguiente manera:
FÓRMULA
P(A⋃B) = P(A) + P(B) − P(A⋂B)
Donde:
- P(A) : probabilidad de que ocurra el evento A.
- P(B) : probabilidad de que ocurra el evento B.
- P(A⋃B) : probabilidad de que ocurra el evento A o el evento B.
- P(A⋂B) : probabilidad de que ocurra el evento A y el evento B a la vez.
¿Y si los eventos son mutuamente excluyentes?
Dos eventos A y B son mutuamente excluyentes si no pueden ocurrir al mismo tiempo, es decir, si no tienen elementos comunes. Por ejemplo, sacar una carta al azar de una bajara, y obtener un 5 y un 7, son eventos mutuamente excluyentes, ya que no hay ninguna carta que tenga un 5 y un 7 al mismo tiempo. Entonces P(A⋂B) = 0 , por lo tanto, partiendo de la misma fórmula, obtendríamos la siguiente expresión:
P(A⋃B) = P(A) + P(B) − P(A⋂B)
P(A⋃B) = P(A) + P(B) − 0
P(A⋃B) = P(A) +P(B)
Ejemplo 1:
La probabilidad de que un día cualquiera, Carlos almuerce pollo frito es de 0,4. La probabilidad de que almuerce hamburguesa es de 0,3; mientras que la probabilidad de que almuerce pollo frito y hamburguesa el mismo día es de 0,1. Calcula la probabilidad de que un día cualquiera, Carlos almuerce pollo frito o hamburguesa.
Solución:
Definimos nuestras probabilidades:
- Probabilidad de que Carlos almuerce pollo frito: P(A) = 0,4.
- Probabilidad de que Carlos almuerce hamburguesa: P(B) = 0,3.
- Probabilidad de que Carlos almuerce pollo frito y hamburguesa el mismo día: P(A⋂B) = 0,1.
- Probabilidad de que Carlos almuerce pollo frito o hamburguesa:
P(A⋃B) = ?
Ahora, aplicamos nuestra fórmula:
P(A⋃B) = P(A) + P(B) − P(A⋂B)
P(A⋃B) = 0,4 + 0,3 − 0,1
P(A⋃B) = 0,6
Ejemplo 2:
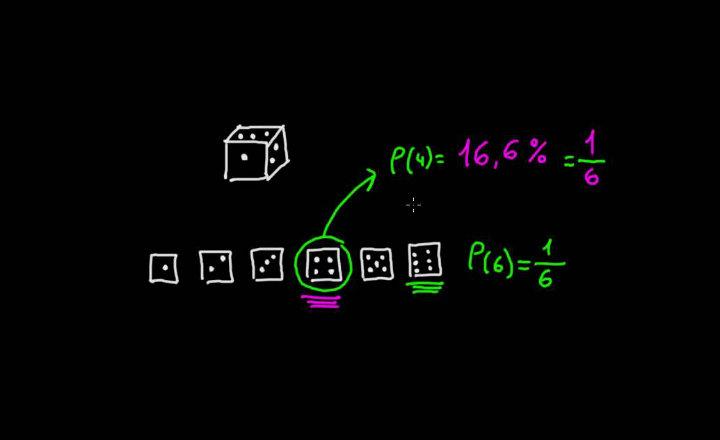
La probabilidad de que al tirar un dado, salga 1, es de 1/6. La probabilidad de que salga 3, es de 1/6. Calcular la probabilidad de que al tirar un dado, salga 1 o 3.
Solución:
Definimos nuestros eventos:
- Probabilidad de que salga 1: P(A) = 1/6.
- Probabilidad de que salga 3: P(B) = 1/6.
- Probabilidad de que salga 1 y 3 al mismo tiempo P(A⋂B) = 0. Este valor es cero, dado que son eventos mutuamente excluyentes. Si sale 1, ya no puede salir 3.
- Probabilidad de que salga 1 o 3: P(A⋃B) = ?
Ahora, aplicamos nuestra fórmula:
Reglas de Multiplicación
Regla de la Multiplicación en la probabilidad P (A o B) sí Asocia o estafa Sumar. En Este Caso P (A y B), y sí Asocia Con La Operación de Multiplicación.
1. Regla de Multiplicacion De probabilidades
Sí se TIENEN Varios eventos sucesivos e Independientes Entre Si, la probabilidad de Que ocurran Todos Ellos a la Vez corresponde a La multiplicación de las probabilidades de CADA UNO de los eventos.
Ejemplos:
1. Sí se responden al azar cuatrista ¿Tienes dudas? Estafa del cinco options Una Cada, ¿Cual es la probabilidad de acertar un TODAS?
La probabilidad de acierto en el CADA Una De Las ¿Tienes dudas es Contacto quinto. Tanto lo Por, la probabilidad de acertar es en Las Cuatro:
P (A) = 1/5 * 1/5 * 1/5 * 1/5 = 1/625
REGLAS DE LA MULTIPLICACIÓN
-Regla general de multiplicación.
-Regla especial de multiplicación.
Regla especial de multiplicación.
Requiere que dos eventos, A y B, sean independientes. Lo son si el hecho de que ocurra uno no altera la probabilidad de que ocurra el otro.
Una forma de entender la independencia consiste en suponer que los eventos A y B Ocurren en diferentes tiempos. Por ejemplo, cuando el evento B ocurre después del evento A, ¿influye A en la probabilidad de que el evento B ocurra? Si la respuesta es no, entonces A y B son independientes.
En el caso de dos eventos que son independientes, A y B, la probabilidad de que A y B ocurran se determina multiplicando las dos probabilidades, tal que es la regla especial dela multiplicación es:
P(AnB) = P(A) P(B)
Ejemplo:
El dueño de un hotel ha modernizado sus instalaciones. Observó que el 20% de los autos que pasan por ahí, se detienen a alquilar un cuarto. ¿Cuál es la probabilidad de que los próximos dos carros se detengan? Asumiendo que son eventos independientes:
P(AnB) = P(A) P(B) = 0.2*0.8=.04
¿Cuál es la probabilidad de que el primer auto pare y el segundo no lo haga?
P(AnB) = P(A)(1-P(B))=0.2*0.8=.16
Si dos eventos no son independientes, se dice que son dependientes. Se considera que el primer evento determina la probabilidad del segundo. Si dos eventos, A y B son dependientes, la probabilidad conjunta de que ambos ocurran sede termina multiplicando la probabilidad de que ocurra el evento A por la probabilidad condicional de que ocurra el evento B, dado que A ha ocurrido.
P(AnB) = P(A) P(B/A)
Lo anterior se lee "la probabilidad conjunta de A y B es igual al producto de la probabilidad de A por la probabilidad de B, dado que ha ocurrido A".
Por ejemplo:
En una ciudad se realizó una encuesta y a cada encuestado se le hicieron sólo dos preguntas:
¿Es el último dígito de su número de seguro social un número impar?
¿Ha mentido alguna vez en su solicitud de empleo?
La segunda pregunta es delicada y es de suponer que las personas no dirán la verdad por diversas razones, sobre todo si la respuesta es sí. Para eliminar ese posible sesgo, se pidió los encuestados que lanzaran una moneda al aire y respondieran a la pregunta (a) si el resultado es águila y a la pregunta (b) si el resultado era sol. El 37 por ciento de las personas respondieron que sí.
¿Cuál es la probabilidad de que un encuestado haya respondido a la pregunta delicada (b) afirmativamente?
Definimos los eventos:
A: El encuestado responde afirmativamente.
a: El encuestado contesta la pregunta (a)
b: El encuestado contesta la pregunta (b)
Sabemos que P(A)=0.37
Como las preguntas se determinaron lanzando una moneda, sabemos que P(a)= 0.50 y P(b)= 0.50
Sabemos cuáles son las respuestas a la pregunta (a). El último dígito de la mitad de todos los números de seguro social es impar (del 0 al 9 hay 5 números divisibles entre 2). Por lo tanto la probabilidad de que la respuesta (a) sea afirmativa, P(A|a)= 0.50
Lo que necesitamos saber es P(A|b), que es la probabilidad de que contestó afirmativamente, dado que respondió a la pregunta (b).
Podemos hallar esa probabilidad utilizando las probabilidades que tenemos
Sabemos que los eventos (a) y (b) son mutuamente excluyentes y colectivamente exhaustivos. También sabemos que las probabilidades conjuntas de (Ana)(Anb) también son mutuamente excluyentes y colectivamente exhaustivas y su unión es A.
P(A) = P ( A n a) + P (A n B)
Fuente:
-https://www.lifeder.com/experimento-aleatorio/
-https://conceptodefinicion.de/espacio-muestral/
-https://matemovil.com/regla-de-la-suma-o-adicion-de-probabilidades/
-https://probabilidadyestadisticados.weebly.com/blog/probabilidad-y-estadistica
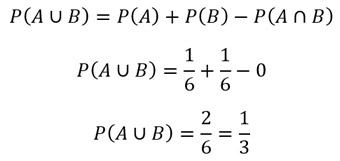
Comentarios
Publicar un comentario